Optimisation non linéaire 2

Aperçu des sections

• 

  Ressources du cours

  
  

  • Annonces Forum
• 

  Section 1

  Dans ce chapitre, on s'íntéresse à la solution numérique des systèmes linéaires qui fait partie de l'analyse numérique matricielle. En effet, il y'a deux types de méthodes de résolution de systèmes linéaires : celles dites directes ; donnant la solution exacte après un nombre fini d'opérations élémentaires, et celles dites itératives ; engendrant une suite de solutions approchées qui converge vers la solution exacte, en se fixant une précision à atteindre.

  • chapitre 1 Fichier
• 

  Section 2

         La modélisation consiste en la traduction et représentation d'une situation concrète en un ensemble de relations mathématiques.

      Pour trouver un tel modèle mathématique, on a trois entités à identifier:

      i) L'ensemble des actions (activités) qui s'offrent à l'agent de décision (variables).

      ii) L'objectif visé exprimé sous la forme d'une fonction mathématique (fonction objectif).

      iii) Les règles définissant la nature du système à l'étude exprimées en termes de relations mathématiques (contraintes).

  
  

  • Chapitre 2 Fichier
• Cette section
  

  TP Optimisation

  Chargé du TP: M. Sahari Mohamed Lamine
  

  mail: mlsahari@gmail.com

  
  

  • Manuel MATLAB Fichier
  • TP N°1 Fichier
  • Animation vidéo URL

    Une animation montrant la convergence lente de la méthode du gradient à pas fixe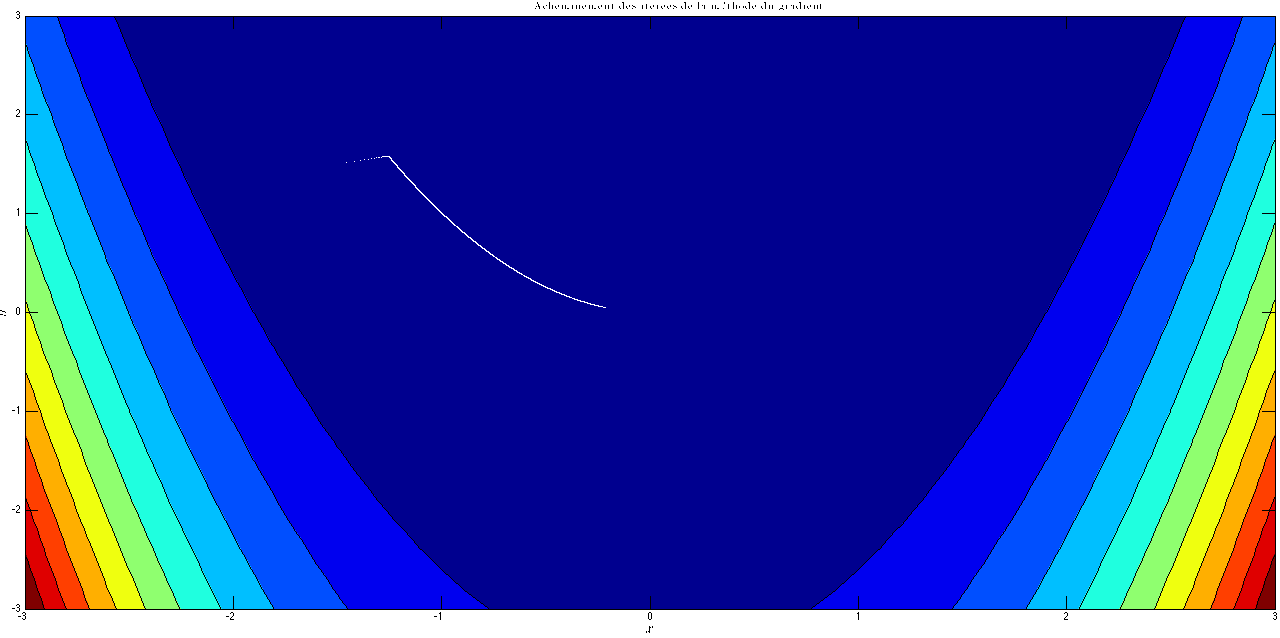

    
    

    
    

  • Le prochain TP:

    • Méthode du gradient dans $\mathbb{R}^n$, $n=1,2,3, ...$
      
    • Méthode du gradient dans $\mathbb{R}^n$, $n=1,2,3, ...$avec recherche linéaire

    
    

  • TP N°3 Fichier

    La méthode du gradient dans $\mathbb{R}^2$ à pas fixe pour la fonction de Rosenbrock:
    

    $f(x,y)=100(y-x^2)^2+(1-x)^2$
    

    • Compléter le code de la recherche linéaire !
      
  • 
    

  • TP N°4 Fichier
  • La méthode du gradient avec recherche linéaire URL
  • Acheminement des itérées de la méthode du gradient avec recherche linéaire

    
    

  • Modifier le code du TP N°4 pour ajouter une recherche linéaire inexacte d'Armijo.
    

    Un pas $t_k$ choisit selon la règle d'Armijo vérifie la condition:

    $\theta(t^{\ast})\leq m\theta^{\prime}(0)t^{\ast}+\theta(0)$
    

    Où $0<m<1$
    

    
    

    
    

  • Modifier le code du TP N°4 pour ajouter une recherche linéaire inexacte de Goldestein.
    

    Un pas $t_k$ choisit selon la règle de Goldestein vérifie les deux conditions:

    $\theta(t^{\ast})\leq m_{1}\theta^{\prime}(0)t^{\ast}+\theta(0)$

    et

    $\theta(t^{\ast})\geq m_{2}\theta^{\prime}(0)t^{\ast}+\theta(0)$
    

    Où $0<m_{1}<\frac{1}{2}<m_{2}<1$
    

    
    

    
    

  • Modifier le code du TP N°4 pour ajouter une recherche linéaire inexacte de Wolfe.
    

    Un pas $t_k$ choisit selon la règle de Wolfe vérifie les deux conditions:

    $\theta(t^{\ast})\leq m_{1}\theta^{\prime}(0)t^{\ast}+\theta(0)$

    et

    $\theta ^{\prime }(t^{\ast })\geq m_{2}\theta ^{\prime }(0)$
    

    Où $0<m_{1}<\frac{1}{2}<m_{2}<1$
    

  • TPN°5 Fichier
  • Dans le code du TP N°5:
    

    1. Ajouter une fonction qui calcul la matrice hessienne de la fonction $f$
       
    2. A l'aide de la fonction matlab inv (voir https://fr.mathworks.com/help/matlab/ref/inv.html) calculer l'inverse de la matrice hessienne en un point donné.
    3. Introduire la direction de Newton donnée par : $t_k=1$ et $d_k=-(H(x_k))^{-1}\,g(x_k)$; où $g(x_k)$  est le gradient en $x_k$ et $H(x_k)$ est le hessien en $x_k$.
    4. Exécuter le code et corriger les erreurs eventuelles